1. A line must be left blank before the beginning and after the end of the entire labeled statement or formal proof. However, a line should not be left blank before or after a new page-separation line or at the beginning or end of a braille page.

2. Theformal proof must begin in cell 3, and its runovers must begin in cell 1.

3. If the formal proof contains subheadings such as Given, Prove, or Conclusion, the subheadings must begin in cell 3, and their runovers must begin in cell 1. A line must not be skipped above a subheading. A subheading should be capitalized or italicized in accordance with the print text. If the subheading is in boldface type, it should be entirely capitalized in braille.
   1. Theorem 1. If two angles of a triangle are equal, the sides opposite these angles are equal.

      Given: Triangle ABC with angle A equal to angle C.
      Prove: BA = BC.
      Look at the braille equivalent in a separate window.

1. A line should be left blank before the beginning and after the end of the step-numbered items.

2. The print columnar form must not be followed in braille. Each item from the Reasons column must be placed beneath its matching item from the Statement column.

3. The letters "S" for Statement and "R" for Reason must be placed immediately after the appropriate step number. Similarly, other column headings should be indicated by appropriate letters.

4. Each step number must begin in cell 1, and any runovers must begin in cell 3.

5. A transcriber's note must be included to explain the change in format to specify the meaning of the letters use to replace the headings. The note must be placed at the beginning of each volume in which a change of format occurs.

1. Theorem 2. All right angles are equal.

   Given: Angle ABC and DEF are right angles.
   Prove: Angle ABC equals angle DEF.
   Proof:

Look at the braille equivalent in a separate window.

Margins for Itemized Material With Subdivisions:

1. In transcribing itemized material with lettered or numbered subdivision, the main item designation must begin in cell 1, and its runovers must begin in cell 5. Each lettered or numbered subdivision must begin in cell 3, and its runovers in cell 5. If any item has more that one paragraph, each new paragraph must begin in cell 7, and its runovers in cell 5.
   1. 1. Use numerals to write the following number sentences.

      a. Fifteen thousand six hundred thirty-two.

      b. Nine million four hundred six thousand.

      Now add the numerals you wrote in a and b. What is the sum?

      Look at the braille equivalent in a separate window.

   2. 2. a. Write each of the following as a fraction: .12; 78.

      b. Tell what digit is in tenth's place.

      Look at the braille equivalent in a separate window.

   3. 3. Consider the theory with primitive notions and operations as stated above. The axioms are the following:

   a. X is an associative operation.

   b. (x X y)'= y' X x'.

   c. If x X y = z X z' for some z, then x = y'.

   (1) Show that the theory is consistent.

   (2) Show that this set of axioms is dependent.

   Look at the braille equivalent in a separate window.

2. It is permissible to place the subdivisions of itemized material side by side across a page if all the subdivisions can be accommodated on one braille line. Otherwise, the format in a above must be used.
   1. 1. Copy and multiply.

      a. 170 X 71    b. 1.25 X 12

      Look at the braille equivalent in a separate window.

   2. 2. Express each of the following as the product of two factors.

      a. 21   b. 36   c. 100

      Look at the braille equivalent in a separate window.

   3. Solve and Check.

      3. a. 4x = 96   b. n + 2 = 8

      Look at the braille equivalent in a separate window.

   4. 4. Factor:

      
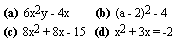
      Look at the braille equivalent in a separate window.

3. When itemized material is arranged in tabular form so that items are numbered at the margin and beneath lettered column headings, the material should be transcribed in one of the following ways:

1. If all the columns can be accommodated across the braille page, the print columnar arrangement must be followed. Each problem number must begin in cell 1. The letter identifying each column must be aligned with the first cell of the realted column. A blank line must be left above and below the lettered column headings. At least two blank cells must be left between columns.

   (1) Find the answers mentally.

   
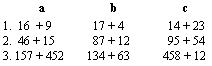
   Look at the braille equivalent in a separate window.

2. If all the columns cannot be accommodated across the braille page, each subdivision in each problem must be lettered individually, and the format in a above must be followed.

   (1) Mixed practice.
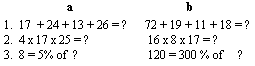